Under deconstruction

Frequency counting in Haskell

by Ketil Malde; November 11, 2013

One of the things I find myself using associative data structures (a.k.a. finite maps, hash tables, …) for again and again, is frequency counts. This is such a common task, and thus it should be easy and efficient, but due to the non-strictness of Haskell, it’s in fact a bit tricky to get right. So if you use a Data.Map (specifically, Data.Map v Int), instead of a simple expression like:

freqtable = foldl' (M.insertWith (+1) 1) M.empty

I often found myself writing something like:

freqtable = go M.empty 
  where
  go m [] = m
  go m (i:is) = let v = M.findWithDefault 0 i m 
                    v' = v+1
                    m' = M.insert i v' m
                in v' `seq` m' `seq` go m' is

The good news is that the contortions above are not really necessary anymore. We now have strict versions of these data structures which always evaluate the value elements, as well as insertWith' (with a tick at the end) which evaluates values (to WHNF) on insertion.

The bad news is that for various reasons, Data.Map isn’t always the optimal data structure for this, and so I decided to investigate a bit.

Candidate data structures

The default data structure for associative maps in Haskell is perhaps still Data.Map, but in many cases, Data.IntMap.Strict is a better choice. This is strict, and by using Int as the key (which isn’t really a severe limitation for most purposes), is more efficient. This is still implemented as a tree structure, which enables sharing and immutability and purity - the usual goodies. (But note that this isn’t so important here - we’ll often just build the table once at the outset and then use it, we’re not updating things much later on.)

Another alternative is a direct table of counts. Data.Vector is Haskell’s new all-purpose arrays, providing a 0-indexed table with various options for content. The older Data.Array provided more flexible arrays with multiple dimensions etc, but these can fairly easily be built on top of vectors. Like Data.Array, vectors come in multiple flavors:

• regular - unboxed, can hold complex (and unevaluated, non-strict) values
• unboxed - stores primitive data structures directly, and is strict
• mutable - can do destructive updates, but requires operations in a monad

Then finally, there is Data.Judy - in fact, stumbling over its Haskell library by Don Stewart is the reason I started looking into this. The C version is advertised as an extremely performant, mutable, cache-friendly tree structure.

Implementation

To benchmark these data structures, I’ve written a small driver program that basically inserts a given number of values from a given range into one of these data structures, and measured CPU time and memory usage with /usr/bin/time.

So, to make it clear, given a range r, and a number of values n, we insert n random values between 0 and r. Since Vector has a predetermined size, we allocate an r-sized array, for the others, the size grows dynamically.

Also, all counts are Ints (or the equivalent Word for Judy), especially Vector could probably save by using a smaller data type for storing counts.

Oh, and Don’s Judy library is a bit sparse, among other things, I added an insertWith. This makes frequency counting a bit faster (see below), as well as thread safe.

Results

Anyway, this is how it looks so far:

 

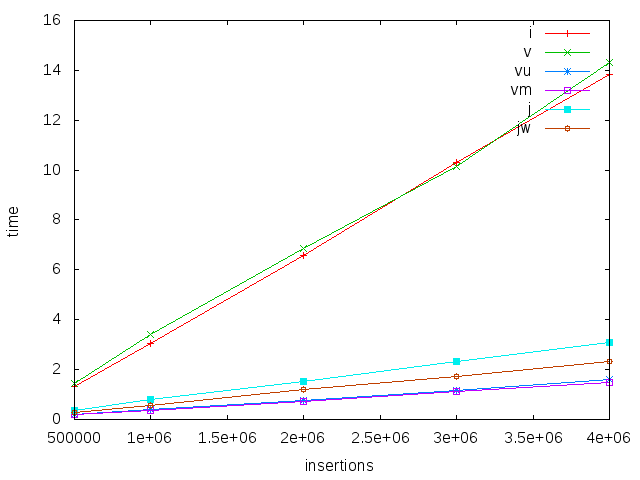
Here we use a fixed range (up to 1M), and vary the number of inserts. We see that all implementations scale linearly - which is what we would expect. IntMap and (boxed) Vector are about seven times slower than the others, though, while unboxed and mutable vectors are a bit faster than Judy (j is Judy with lookup and insert, jw is judy using insertWith)

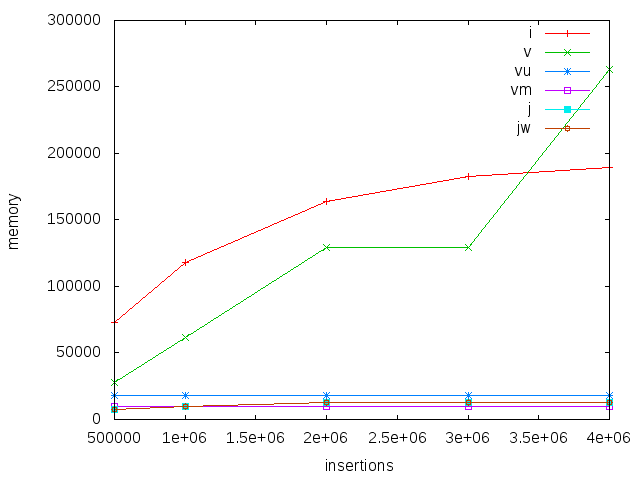
Memory consumption is lowest and constant for mutable and unboxed vectors. Judy has a comparable low memory footprint, but grows slightly with number of inserts. IntMap is way more expensive, something like 20x bigger. Interestingly, boxed vector seems to use a large amount of memory, I’m not exactly sure why this is.

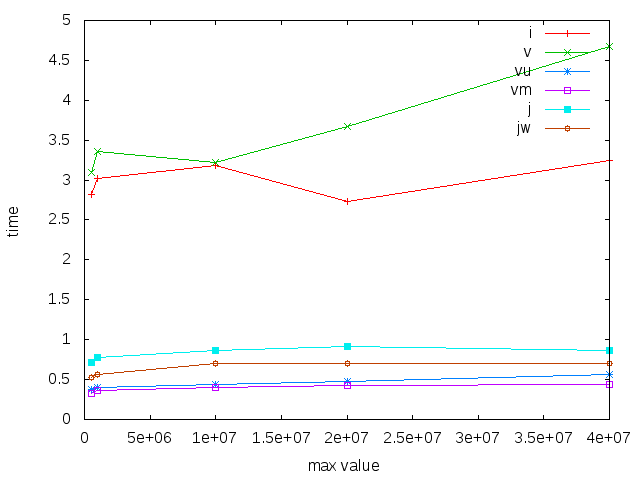
Of course, vectors are fast when you can allocate a relatively small array, and update it directly. But the price you pay is limited range, here we look at how a constant number of insertions (again 1M) look when we increase the range. Again, IntMap and boxed vectors are slow, Judy and the other vectors are substantially faster.

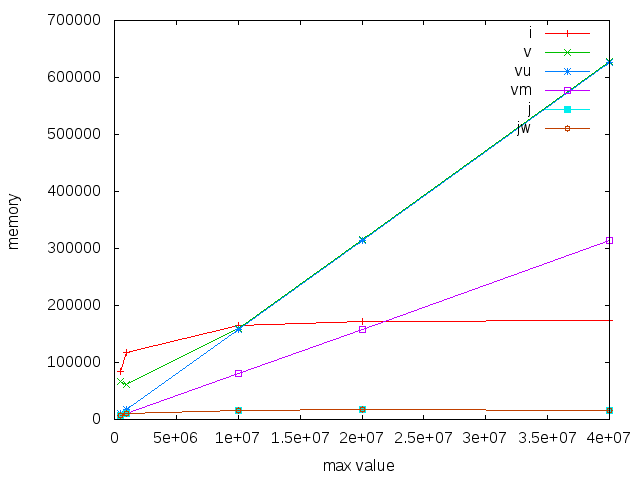
Finally, we see that for memory use, vectors scale linearly with the range. Interestingly, the mutable vectors have half the memory footprint of immutable, but unboxed vectors. I would have thought an unsafeFreeze or equivalent would make them the same - but apparently not? And Judy really shines here, with a tiny footprint compared to the others.

Conclusions

For small ranges and dense data (relatively few counts of zero), use Data.Vector, the mutable kind. For large ranges and/or sparse data, use Data.Judy.

A version of Judy that compiles on recent compilers, and adds some extra functions (e.g., insertWith and adjust) can be found here. Scripts etc used in benchmarking are here. I haven’t spent a lot of effort exploring implementation options, so it is likely that my implementations are suboptimal. As always, comments welcome.

comments powered by Disqus