Calculating insert stats from BAM files
by Ketil Malde; September 11, 2012
Given a set of reads, the first step of analysis is almost always to align them to a reference. Today, this means running some specialized aligner - I generally use bwa - which results in a BAM file. The next step is (or should be) to check the result, and I wrote a small tool for this purpose.
Basic operation
A pair of reads is classified in one of four classes. First, “innies” have the reads pointing inwards, i.e. the mate of a read is found downstream and on the reverse-complement strand. This is the normal orientation for paired-end reads. “Outies” point outwards, this is the result of mate-pair protocols that circularize and clip the insert before sequencing. Finally, “lefties” are oriented the same way with the first read upstream of the second, and “righties” point the same way, but with the second read upstream.
We support calculating statistics on the distribution of insert lengths (bam stats), a histogram (bam hist), or quantiles (bam quant). It is also possibly to simply dump the contents of the BAM file in SAM format - sorted by orientation of the pairs (bam dump), this is mostly for debugging purposes..
Examples
It is probably just as easy to document this by example, so here goes:
Distribution stats
% dist/build/bam/bam stats 0207.bam
Alignment count prop mean stdev skew kurt
innies 161010 46.00% 37351.9 4099.5 0.1 0.1
outies 0 0.00% NaN NaN NaN NaN
lefties 6 0.00% 28524.8 27577.8 0.2 -1.9
righties 0 0.00% NaN NaN NaN NaN
Total reads: 700106Here we see that most of the mapped reads are “innies”, with a mean insert length of 37K (it’s a fosmid library, so this is as expected), and a very nice normal distribution as seen from the skew and kurtosis columns.
Quantiles
The mean can be deceptive when dealing with skewed distributions, and often it is more useful to use median - and by extension, quantiles.
% bam quants tmp/inbred-110415_8-mp2.bam
Alignment count prop 5% 25% 50% 75% 95%
innies 4491570 9.38% 200 281 393 1696 4289
outies 17652491 36.86% 530 1206 1843 2549 3627
lefties 30334 0.06% 699 5355 16625 51108 332782
righties 33161 0.07% 721 5431 17111 47540 339773
Total reads: 95771572The data is from a mate-pair sequencing protocol, but fairly typically, it isn’t very reliable, and it gives a pretty high proportion of regular paired-end reads. It also maps relatively few pairs.
Histogram
% bam hist -b 5 -n 1e6 100910_s_3_GLW-1.bam
Alignment count prop 200 400 600 800 >
innies 396093 79.22% 14229 324953 55744 984 183
outies 22839 4.57% 146 262 331 775 21325
lefties 891 0.18% 85 152 121 107 426
righties 879 0.18% 49 131 113 117 469
Total reads: 1000000This is ostensibly a mate-pair library, but as we can see, it’s mostly regular paired end reads with lenghts between 200 and 400bp.
Note that we used -n to limit the number of reads (for expediency), and -b to limit the number of buckets (for clarity of presentation).
Histogram plots
Histograms are good candidates for plotting, and there’s a --plot option that generates output suitable for piping into gnuplot. This option takes an optional string argument which is passed to gnuplot, so you can use it to inject gnuplot commands (e.g. to plot only innies, do --plot='set xrange [0:]; set yrange [0:]'. Or to output to a file, do --plot='set out "file.jpg"; set term png'.) Output can be piped to gnuplot --persist, or redirected to a file.
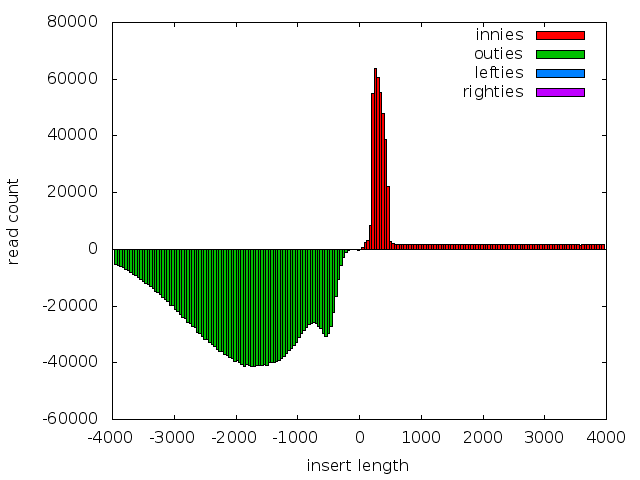
An example plot for the mate-pair sequences. Note a large fraction of ‘innies’ remain, and that the distribution of ‘outies’ looks to be bimodal.
Performance
Parsing through a large BAM file takes a few minutes, over five on my PC for 200M reads (14Gb of compressed data). You can use the -n option to limit the number of reads processed, this usually gives you a good approximation quickly.
Notes on implementation
Since we’re dealing with potentially large files, everything is calculated by streaming through the data. This way, the memory footprint is low.
For distribution statistics, I’m using the standard trick from SAS’s UniVar method. We first calculate (simultaneously) the number of data points, their sum of x, sum of squares, sum of cubes, and sum of fourths, and at the end, we derive the various measures.
Histograms are of course trivial, using a set of buckets, we just fill them up as we go along.
Quantiles are a bit tricky, there’s a review on WP of how this can be done, but most methods either require storing the data, require multiple passes, or are complicated and slow. In the end, I settled for an approximate variant, based on the histogram code. We use a set of buckets (this time with slightly increasing sizes), and identify the correct bucket for each quantile. We then interpolate to get the quantile value.
Interestingly, I accidentally forgot to limit the number of buckets generated. To my surprise (and then embarrassement at being surprised), it worked nicely. Laziness, of course, allows an infinite sequence of buckets, and as long as you don’t look for quantiles above 100%, this will work.
Availability
As usual, bamstats is on hackage, or you can get a copy with darcs get http://malde.org/~ketil/biohaskell/bamstats (or just browse the source archive). I’ve also mirrored the repository on hub.darcs.net, at the moment this is an experiment, but if it works out well, this could be the new official home.
Let me know if you find the program useful!
comments powered by Disqus

